UFC 4-023-03
25 January 2005
undergo significant rotation, add an equivalent plastic hinge to the model, by inserting a
discrete hinge at the correct location within the member. Insert the hinge at the correct
offset from the member end; use engineering analysis and judgment to determine the
offset length, which must be less than the depth of the member from the face of the
column. Also, apply two constant moments, one at each side of the new hinge, in the
appropriate direction for the acting moment; see Figure 3-9. For Nonlinear Static and
Dynamic analysis, use software capable of representing post-peak flexural behavior.
Ensure that shear failure will not occur prior to developing the full flexural design
strength. Additional guidance on the modeling of plastic hinges in reinforced concrete
can be found in Plastic Methods for Steel and Concrete Structures (Moy 1996) and
Reinforced Concrete: A Fundamental Approach (Nawy 2000).
If the structural element is not able to develop a constant moment while
undergoing continued deformations, remove the element when the internal moment
exceeds the flexural design strength. Redistribute the loads associated with the
element per Section 3-2.4.3.
4-3.1.2
Combined Axial and Bending Resistance of Reinforced Concrete.
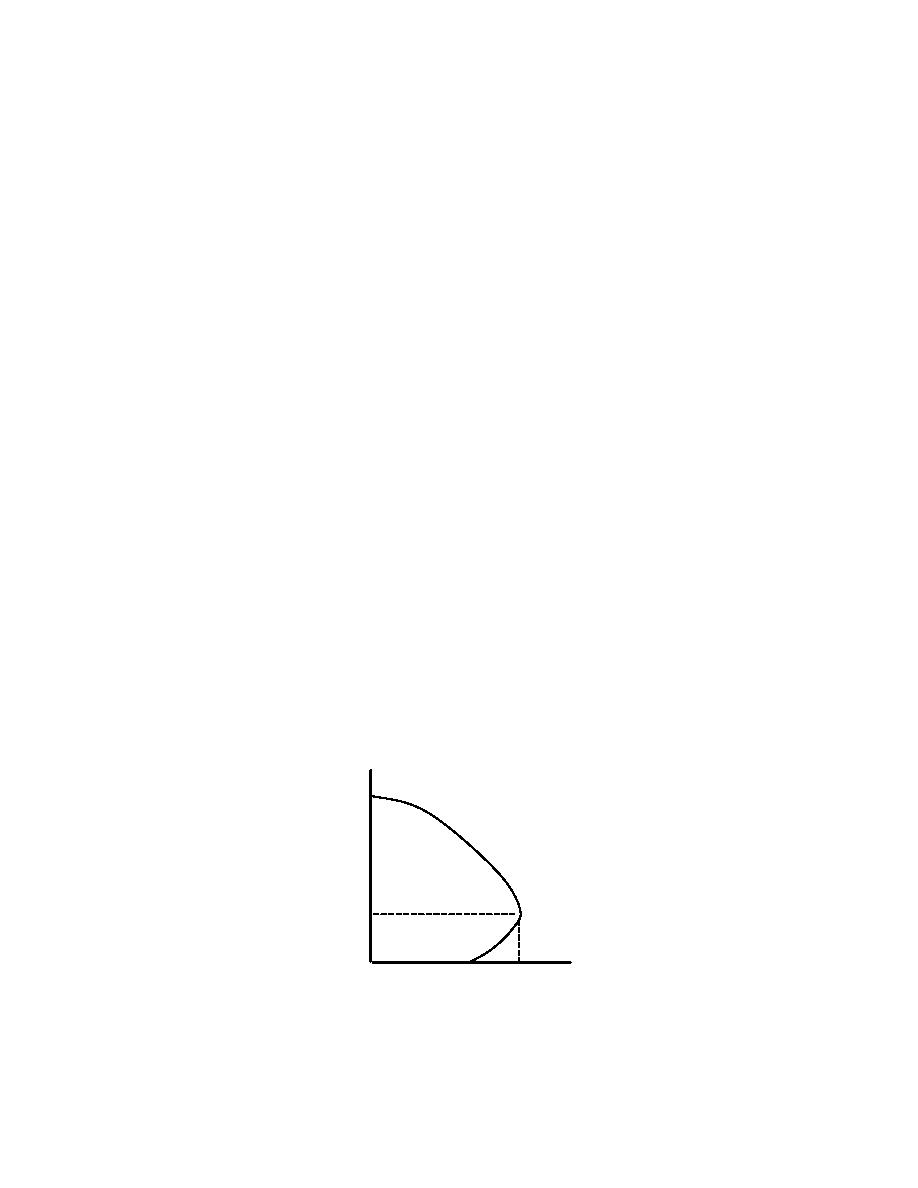
The acceptability criteria for elements undergoing combined axial and
bending loads are based on the provisions given in Chapter 10 of ACI 318-02, including
the appropriate strength reduction factor Φ and the over-strength factor Ω. If the
combination of axial load and flexure in an element exceeds the design strength and the
un-factored axial load is greater than the nominal axial load strength at balanced strain
Pb, remove the element and redistribute the loads associated with the element per
Section 3-2.4.3; see Figure 4-1. If the un-factored axial load is less than Pb, then insert
an equivalent plastic hinge into the column, per the procedure discussed in Section 4-
3.1.1.
Figure 4-1 Axial Load and Moment at Balanced Strain
P
Pb
M
Mb
4-7



 Previous Page
Previous Page
